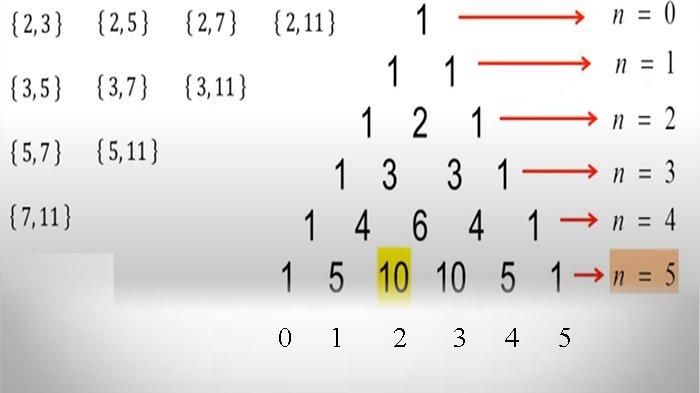
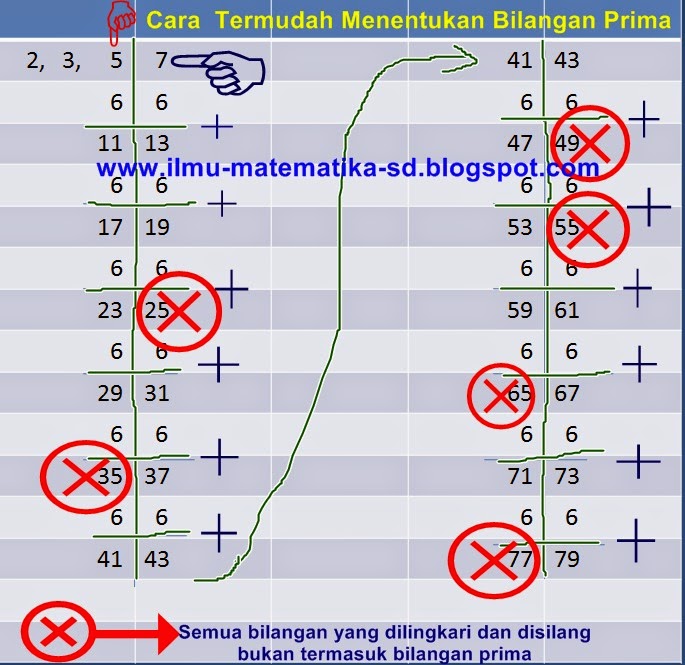
2 3 5 7 11
Nyatakan Dengan Notasi Pembentuk Himpunan K 2 3 5 7 11 13 Brainly Co Id
Dinyatakan Dengan Menyebut Anggotanya K 2 3 5 7 11 13 Dinyatakan Dengan Menuliskan Sifat Ke Brainly Co Id
Misal A 2 3 5 7 11 13 17 19 A Jika Dinyatakan Dalam Notasi Pembentuk Himpunan Brainly Co Id
Diketahui Suatu Barisan 3 5 7 9 11 Un Tentukan Rumus Suku Ke N Kemudian Tentukan Suku Brainly Co Id
Makasih Loh Brainly Co Id
Jawaban Buku Matematika Kelas 8 Ayo Kita Berlatih 1 4 Hal 22 Tentukan 3 Bilangan Selanjutnya Pentium Sintesi
The last digit is 0 2 4 6 or 8.
2 3 5 7 11. 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97. 2 2 1 3 3 2 5 5 2 7 7 4 11 11 2 13 13 4 17 next term 17. So the next prime numbers after 11 are 13 then 17 19 23 29 31 37 41 43. Divisibility test for 2.
However the sequence 2 3 5 7 11 are the first five prime numbers. Divisibility tests for 2 3 5 7 and 11. The number 0 is not a prime number. One is has one divisor itself.
Divisibility test for 3. Choose the correct alternative that will same pattern and fill in the blank spaces. A prime number is a positive integer which has exactly 2 positive integer factore one factor being 1 and the other factor is the positive number itself. 2 2 133 3 113 7 75 5 7can t be done with 3 different primes there s no way to make 17 from 2 3 5 7 11 13 another answer 19 13 11 17.
This shows you the divisibility tests for 2 3 5 7 and 11 so you can tell if those numbers are factors of a given number or not without dividing. 2 3 5 7 11 13 17 3 2 1 5 3 2 7 5 2 11 7 4 13 11 2 17 13 4 therefore the next number is obtained thus. Is 0 a prime number. Is 1 a prime number.
Is 2 a prime. Zero is not a positive number and has infinite number of divisors. 2 3 5 7 11 x 17 in number series question a number series is given with one term missing.
Rangkuman Dan Jawaban Matematika Himpunan Belajar Dari Rumah Tvri Kamis 23 Juli 2020 Semua Halaman Kids
Tentukan Rumus Suku Ke N Untuk Setiap Barisan Berikut A 2 5 7 11 14 B 9 7 5 3 1 Brainly Co Id
Cara Mencari Bilangan Prima Teknologi Berbasis It Pada Perkembagan Aplikasi Digital
Kuis Matematika Deret Angka 2 3 5 7 11 13 19 Coba Jawab Dan Berikan Penjelasannya
Page 61 Ayo Belajar Mtk 4
5 3 5 2 3 5 9 7 Brainly Co Id
Cara Mengerjakan Deret Angka 1 1 3 2 5 3 Guru Ilmu Sosial
Bilangan Bulat Dan Romawi 2
Http E Soal Alazhar Kembangan Sch Id Index Php Catalog Download Filename Barisan Dan Deret Bilangan Pdf
Jawaban Buku Paket Matematika Kelas 7 Semester 2 Halaman 130 Guru Ilmu Sosial
Bilangan Prima 1 100 Pengertian Rumus Contoh Soalnya
Contoh Soal Himpunan
Diketahui Barisan Bilangan 3 5 7 9 11 Tentikan A Suku Ke N B Suku Ke 50 C Jumlah 50 Suku Brainly Co Id
