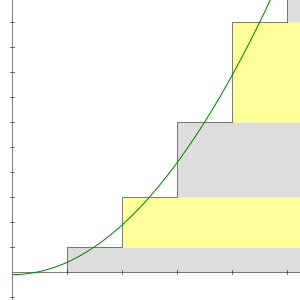
1 2 3 4 5 6 N 1 12 Proof
The euler maclaurin formula bernoulli numbers the zeta function and real variable analytic continuation by terence tao.
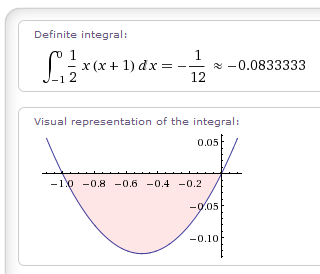
1 2 3 4 5 6 n 1 12 proof. Maths then the answer to this sum is 1 12. How could i have screwed up so badly. C 1 2 3 4 5 6 7 8 4c 0 4 0 8 0 12 0 16 subtracting we get. That is the series doesn t converge to 1 12 but i am still intrigued by the possibility suggested by the numberphiles that it truly equals 1 12 if all the terms out to infinity are included in the sum.
Recently a very strange result has been making the rounds. Keep reading to find out how i prove this by proving two equally crazy claims. And 1 12 have a relationship with each other but certainly don t equal each other update 2 6 14. If you watch the first proof posted he points out that they are ignoring the actual boundaries of the parent equation minute 2.
Smart news keeping you current the great debate over whether 1 2 3 4 1 12 can the sum of all positive integers 1 12. Basically they simplified an equation left out the boundaries and left out the specific conditions s 1 for example. The simplest non rigorous proof is due to srinivasa ramanujan and goes roughly as follows. Euler s proof that 1 2 3 1 12 by john baez.
It says that when you add up all the natural numbers maths 1 2 3 4. The idea featured in a numberphile video see below which claims to prove the result and also says that it s used all over the place in physics. John baez september 19 2008. What is finally left is the above statement.
The analytic continuation of a function is unique so nailing down ζ s for s 1 is all you need to continue it out into the complex plane. The only thing about complex numbers you ll need to know here is that complex numbers are pairs of real numbers regular numbers a and b. People found the idea so astounding that it even made. 1 1 1 1 1 1 1 2.
So i was wrong. It can sort of.

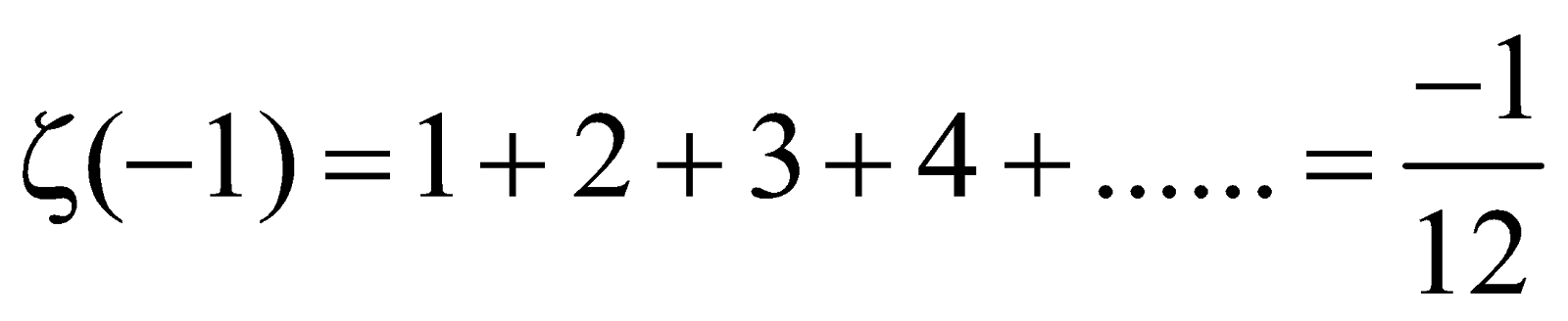


.png)