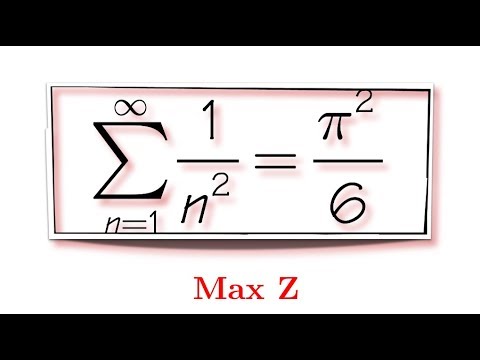1 1 2 1 4 1 N Sum Formula

System out println sum of the series upto num terms is sum instead of using typecasting why didnot you take double type it is easier than type casting.

1 1 2 1 4 1 n sum formula. Multiplying s n by 2 reveals a useful relationship. Regardless of anything else the function itself must converge to 0 as n inf for the sum to converge. Program to find length of bridge using speed and length of train. This converges to 2 as n goes to infinity so 2 is the value of the infinite sum.

Since this is a power series the test for convergence of the sum is very easy. Lim 1 n n inf 0. I won t go into a full explanation as it too complex. Of course one reason for creating the digamma function is to make formulae like this true.

Program to find the sum of the series 1 a 2 a 2 3 a 3 n a n. In your example the finite sums were 1 2 1 1 3 2 2 1 2 7 4 2 1 4 15 8 2 1 8 and so on. Following is the implementation of simple solution. Sum of the reciprocals of the squares sum r 1 n 1 r 2 pi 2 6 sum r 1 n beta k n 1 k where beta x y is the beta function.

Program to find sum of the series 1 3 3 5. One can write 1 frac12 frac13 cdots frac1n gamma psi n 1 where gamma is euler s constant and psi is the digamma function. Thus the value of the infinite sum is a 1 r and this also proves that the infinite sum exists as long as r 1. Sum of the reciprocals sum r 1 n 1 r h n where h n is the nth harmonic number.

The nth finite sum is 2 1 2 n. Subtracting s n from both sides. 2 c program to find sum of the square of all natural numbers from 1 to n. A simple solution solution is to initialize sum as 0 then run a loop and call factorial function inside the loop.

If the function does converge to 0 then the sums might more tests are needed. . How to find 9th n for the below formula h n r 1 1 r 1 2 r. So the the sum might converge.